『仕事の９割は数学思考でうまくいく』【要約】

ビジネス

コンセプト

数学思考はビジネスパーソンの強力な味方。

本の目次

第１章　頭のいい人は「数学」をうまく使っている
数学思考で道は開ける

№１　「数学嫌い」は仕事で損をする

№２　「なぜ？」と思った数だけ仕事はうまくいく

№３　話下手も数学で「完治」する

№４　周りより「一手先」が読める

№5　「アイディア」のスイッチをＯＮにする

№６　「数学思考を今から身につける２つのコツ

第２章　決断力・選択力がアップする数学思考
仕事も数学も決断がすべて

№１　「見切り発車」が発想の幅を狭くする

№２　「鳥の目」で眺めてみる

№３　決断の根拠は「指標化」する

№４　データの「ワナ」にダマされない

№５　数学的推論で「可能性」を広げる

№６　やり直しは「０」からでなくてもいい

第３章　ビジネス表現力を強化する数学思考
言葉に頼らず、グラフを使え

№１　説得したいときこそ「数字」を使う

№２　グラフは「小学生の延長レベル」が効果大

№３　メモは「チャート図」で書き留める

№４　情報の「図式化」で提案の質が上がる

№５　「物事の本質」はなにかを見極める

№６　「割合」の見せ方が賞賛を決める

№７　「言葉の意味」がお互いに理解できているか

第４章　発想力・アイディア脳を磨く数学思考
推理・条件整理の先にアイディアが生まれる

№１　「求められているものは何か」を理解してから考える

№２　アイディアは「直感」ではなく「予測」から生まれる

№３　「分析」の精度が「結果」の精度

№４　「仮説」は結果への近道

№５　「加法」「乗法」から新たなチャンスが生まれる

№６　「立体」で考えると頭がやわらかくなる

第５章　自分力を高め地頭を強くする数学思考
できる人は数学脳で考える

№１　物事は「ざっくり」と考える

№２　できる人は「ショートカット」を選択する

№３　「複眼力」を使って同時並行で処理する
　
№４　「逆算」から創造する

№５　答えは「一つ」解き方は「無限」

文章題と伝え方の関係

文章題を解くのがうまい生徒は、話し方も上手です。文章題を解くためには、情報を整理し式を作り、あるいは図形を描き、答えを導き出します。

これは話をするときに必要なスキルになります。

意図を的確に伝えるためには、話す内容を整理・加工・視覚化（順序・強弱・取捨選択・まとめ）する必要があります。

これはビジネスを円滑に進めるための報告・連絡・相談というコミュニケーション能力向上に役立ちます。

プレゼンに於いても、、数学思考を用いることにより、競合他社に一歩先んじることが可能です。

間違えたところからやり直す

うまくいかなかった場合、失敗をなかったことにして最初からやり直すのではなく、

復元ポイントまで戻り、なぜ間違えたのかを検証することで成長につながります。

算数・数学の指導を通して、間違えた時の生徒のやり直し方は、大きく分けて２通りあります。

１.失敗を検証することなく最初からやり直す。

間違いを把握・分析しない。自分の実力・習性・クセを知ることができない。

情報のストックができず、経験の積み重ねも不可能になり、同じ間違いを繰り返し、成長できない。

２.内容・手順を見直し、ミスした部分を捉えそこから改めて考える。

どこで、なぜ、間違えたのかを振り返る。自分の弱点を見つけ、克服することができる。

同じ間違いを防ぐことが可能になり成長できる。

焦って最初から白紙の状態からやり直すのではなく、失敗した原因、タイミングに、しっかり目を向け取り組むことが仕事においても大事です。

復元ポイントからやり直す問題

【問題】

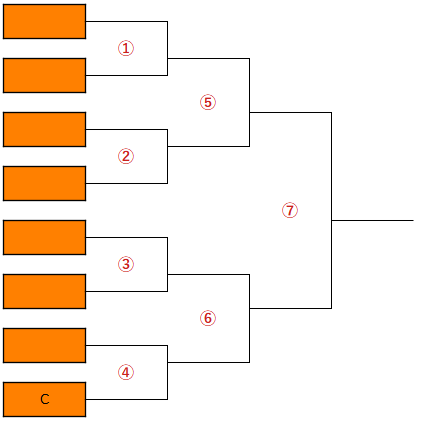
Ａ、Ｂ、Ｃ、Ｄ、Ｅ、Ｆ、Ｇ、Ｈの８チームが、下のトーナメント表の通りに試合を行いました。

次の条件から④で対戦したチームはどこか答えなさい。

条件

・ＡはＤに勝ったがＨに負けた
・ＥはＢに勝ったがＨに負けた
・ＧはＦに勝ったがＡに負けた

トーナメント表

【解答】

まずは全体像を把握します。

このトーナメントで必要なことは、３勝で優勝、２勝すれば決勝戦⑦に進出できること。

これを念頭に３つの条件と照らし合わせると、

ＡはＤとＧに勝っているので決勝進出。

ＨはＡに勝っているので優勝。
ここまでが復元ポイント１

次にこのトナーメントを①と②、③と④のグループに大別するとシンプルになりわかりやすく
なります。

上記よりＡとＨが同じグループになることはありません。

さらに、Ａに１回戦あるいは２回戦で敗退しているＤとＧはＡと同じグループに属します。

しかもＧと対戦したＦも必然的にＡと同じグループになります。

つまり、ＡＤＦＧが①と②のグループになります。

ここが復元ポイント②になります。

問題文と上記より、残りのＢＣＥＨが③と④のグループになります。

３試合戦っているのはＡとＨのみなので、条件よりＥとＨの試合は２試合目。

つまり、⑥に該当します。

そして、Ｅの１試合目の相手はＢなので、自動的に③になります。
したがって④でＣと対戦したのはＨとなります。

正解はＨです。

物事の本質を見極める

事象を正確に把握して、仕事をしているかどうかは、成果に直結します。

本質を見定めるには、思考のクセを修正し、正しい思考回路を作る必要があります。

「速さの平均」と「平均の速さ」は違う

【問題】

片道１２キロのＡ町とＢ町の間を歩いて往復する。

行きは時速６キロ、帰りは時速４キロで歩いたとき、平均の速さを求めなさい。

【解答】

「４と６の平均だから５キロ」と答えた方、不正解です。

５キロは「速さの平均」であって「平均の速さ」ではないからです。

正解は

歩いた距離は合計２４キロ。行は２時間、帰りは３時間かかっているので

２４÷（２＋３）＝４.８キロ

なぜなのか本質を問う問題

【問題】

分数同士の割り算の仕方を説明してみましょう。

５/６÷２/３を計算するときに５/６×３/２とすればよいのか理由を説明してみましょう。

＜ヒント＞

１０÷５と１００÷５０と１０００÷５００はすべて２となることに注目してください。

【解答】

ヒントから１０÷５と（１０×Ａ）÷（５×Ａ）は同じです。

Ａが１０でも１００でも答えは２です。

分数計算でも５/６÷２/３と、（５/６×Ａ）÷（２/３×Ａ）の計算結果は同じになります。

ここで、１０÷１＝１、１００÷１＝１００です。

割り算は割る数を１にすれば簡単です。

２/３×Ａを１にするには２/３×３/２です。

Ａ＝２/３です。

したがってこの計算は

５/６÷２/３＝（５/６×Ａ）÷（２/３×Ａ）

＝（５/６×３/２）÷（２/３×３/２）

＝（５/６×３/２）÷１

＝５/６×３/２

正解　５/６÷２/３＝５/６×３/２が成り立つ

１９９９年、東京大学入試問題。

「サイン（sin)、コサイン(cos)の定義を書け」

三角比に関する公式やテクニックだけでは解答できない問題です。

なぜなのかという本質が、これからは大事だという東大からの強烈なメッセージと受け取られます。

発想力のＰＤＣＡサイクルとは

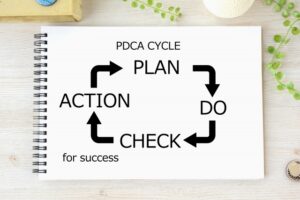
PDCAサイクルとは、業務改善のための技法です。

①ＰＬＡＮ（計画）

実績、予測に基づき、計画を作成する。

②ＤＯ（実行）

計画に沿って業務を遂行。

③ＣＨＥＣＫ（評価）

内容、結果の達成度を点検する。

④ＡＣＴ（改善）

未達成の問題点、原因を探り修正・改善を図る。

①ＰＬＡＮ、②ＤＯ、③ＣＨＥＣＫ、④ＤＯをできるだけ速く回し、継続的に業務の質・効率改善を目指します。

これを発想力を磨くためのサイクルと考えた場合、

予測力→ＰＬＡＮの精度向上

分析力→ＰＬＡＮ、ＤＯの精度向上

仮説力→ＣＨＥＣＫ能力の向上、復元ポイント設定により時間効率向上につながります。

仮説は予測、分析を基に立てて行きます。

目標地点のチェックをすることで具体的に方向性のズレ、ブレを早めに検知して、修正をかけることができます。

仮説を立てることは復元ポイントを設置することになります。

有効な仮説を立てるためには、予測力、分析力の実力をつけることが重要です。

仮説を立てなければ解けない問題

【問題】

Ａ、Ｂ、Ｃ、Ｄ、Ｅの５チームでサッカーのリーグ戦を行います。

どのチームも他のチームと必ず１回ずつ対戦します。

どのチームも１日１試合だけ行います。

大会は５日簡で終了します。

Ａは１日目から４日目まで対戦があり、Ｂ、Ｃ、Ｄ、Ｅの順に対戦します。

１日目にはＥの対戦がありません。

２日目にはＤの対戦がありません。

３日目に対戦がないチームと５日目にＢと対戦するチームをそれぞれ答えなさい。

【解答】

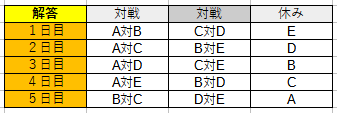
問題文からの情報（条件）を図式化すると表１のようになります。

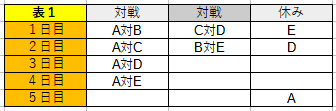
表１から３日目に試合がないのは「ＢまたはＣ」です。

ここで、３日目にＣの試合がないと仮説を立てます。

すると、「Ｂ対Ｅ」が２日続いてしまい条件に反してしまいます。

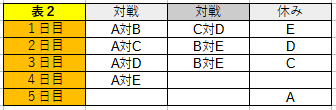
したがって３日目に試合がないのはＢと判明します。

４日目の休みはＣとなります。

そして４日目、Ｂの対戦相手はＤとなります。

よって５日目にＢと対戦するのはＣであることがわかります。。

正解

３日目に試合がないのはＢ
５日目にＢと対戦するのはＣ

仮説を立てて検証した結果、条件に合わなければ、誤りがあることがわかります。

仕事が頓挫したときには、最初に戻るのではなく、仮説を立てた復元ポイントに戻ることで、着実に無駄なくゴールにたどり着くことができます。

ざっくり考える

哲学者、数学者のデカルトの言葉。

「困難なことはすべて扱うことができ、解決が必要な部分へと分割せよ」

物事は分割し、シンプルにした方がわかりやすくなります。

だからと言って、物事を細分化し過ぎるとキリがありません。

ざっくりシンプルに分割するコツ

ひとつひとつの作業ごとに分けるのか。

個別ケースの共通点を見つけて、似た作業グループに分けるのか。

分け方により、進捗具合に相当差が出てきます。

分割する量が多ければ多いほど処理量が増加します。

簡略化するために分割したのに処理量が増えてしまっては、意味がありません。

分割するコツは、大局観を意識して、ざっくり分けることです。

大局観とは物事の総体的な現状や　進展状況を踏まえて的確な形成判断を行う能力のことです。

数学の「場合分け」の思考法が役に立ちます。

根拠をもってザックリ分ける問題

【問題】

①ａ、ｂを自然数としたとき、次のことを示しなさい。

ａ²を３で割ると余りは０または１である。

②２以上の自然数ｎに対し、ｎとｎ²＋２がともに素数になるのはｎ＝３の場合に限ることを示しなさい。

条件は「素数」でること。「自然数」であること。「ｎ²」であること。

素数とは。

５、７、１１、１３、１７のように、２つの数の掛け算をしたときに「１×その数字」でしか表せない数のこと。

１でない自然数。無数に存在していると考えられる。

自然数とは。

正の整数のこと。

ｎ²とは。

ｎ×ｎのこと。

【解答】

上記の定義を整理して「自然数を３で割った余りは２、１、０しかない」ことを考慮すると、

膨大な素数を３つのグループに分けることができます。

自然数全体を３で割った余りに大別して検証します。

Ａ）ａを３で割った余りが０（ａは３、６、９など）→ａ²を３で割った余りは０

Ｂ）ａを３で割ると余りが１（ａは４、７など）→ａ²を３で割った余りは１

Ｃ）ａを３で割ると余りが２（ａは５、８など）→ａ²を３で割ると余りは１

①の正解

よって、ａ²を３で割った余りは必ず０か１になる。

Ｄ）ｎを３で割った余りが０（ｎは素数だから該当は３のみ）

→ｎ＝３のとき、ｎ²＋２＝１１、条件を満たす。

Ｅ）ｎを３で割った余りが１（ｎは素数７、１３など）

→ｎ²＋２は３の倍数になるので不可。

Ｆ）ｎを３で割った余りが２（ｎは素数５、１１など）

→ｎ²＋２は３の倍数になるので不可。

②の正解

よって、ｎとｎ²＋２がともに素数になるのは、

ｎ＝３の場合のみに限定される。

様々なことが起こる仕事も、無策に一つひとつこなしていくのではなく、共通項を見出し根拠のあるグループ分けを行うことで、スマートに効率よく進めることができます。

まとめ

「なぜ」を問い本質に迫る真の数学思考を、仕事に取り入れることの重要性を学べます。

分析力、予測力、発想力、指標化、推論、仮説、グラフ化、図式化、立体化、逆算といった様々な思考法を数学の問題を解きながら、理解できるように試みられています。

数学の公式、解法テクニックを覚えて問題に適用、当てはめて解く能力は、高度経済成長期には必要な能力だったかもしれませんが、今は「なぜ」を繰り返し、自分で考えて本質を見抜く、数学本来の思考法が、仕事にも求められる時代だと思います。

読書に勉強、アウトプット、運動と色々がんばっているけれど、いまいち自己成長できないのは、数学思考が不足しているかもです。

出版情報

著者　　　秋田　洋和

発行日　　２０１３年５月２９日

発行所　　株式会社あさ出版

定価　　　１４００＋税
スポンサーリンク

コメント

タイトルとURLをコピーしました