文系プログラマーのためのPythonで学び直す高校数学

この記事の目次

【目次】
［TryPython］の実行例
【まとめ】
著者プロフィール
【出版情報】

【目次】

第１章コンピュータと「数」

1⃣位取り記数法

1.1　10進位取り記数法
1.2　〇〇の0乗
1.3　2進位取り記数法
［TryPython］10進数から2進数へ
［コラム］〇進法と〇進数
1.4　16進位取り記数法
［TryPython］10進数、2進数から16進数へ

2⃣基数変換

2.1　10進数から2進数へ
［TryPython］10進数から2進数に変換するプログラム
2.2　10進数を16進数に
［TryPython］10進数から16進数に変換するプログラム
2.3　10進数や16進数を2進数に
［TryPython］ほかの位取り記数法から10進数に変換するプログラム

3⃣コンピュータの世界の数字のお話

3.1　データの扱い方
［コラム］ゼロで埋めることの意味
3.2　扱える値には限りがある

4⃣負の数の扱い方

4.1　X＋1＝0を計算する
4.2　2の”補数”て何だ？
4.3　符号ビットで正負を見分ける
4.4　どこまでの値を扱える？
［コラム］数値を扱うデータ型
4.5　2の補数と基数変換
［TryPyton］2の補数を調べる

5⃣実数の表し方

5.1　桁は重みがある
5.2　実数を基数変換する
［TryPython］10進数の実数を2進数に変換するプログラム
5.3　コンピュータは浮動小数点を扱う
5.4　避けられない実数誤差

6⃣文字や色の扱い方

6.1　コンピュータは文字をどう扱うか
6.2　コンピュターは色をどう扱うか

第２章コンピュータの「演算」

1⃣算術演算はコンピュータの四則演算

1.1　計算式の書き方
［コラム］複合演算子
1.2　計算の優先順位
［コラム］()の役割
1.3　実数誤差を減らす工夫

2⃣シフト演算で掛け算・割り算

2.1　桁を左右に動かす
［コラム］シフト演算と算術演算
2.2　右シフトには「算術」と「論理」の2種類

3⃣コンピュータに特有のビット演算

3.1　ビット演算とは
［TryPython］ビット演算を実行してみよう
3.2　AND演算
3.3　OR演算
3.4　XOR演算
3.5　NOT演算
［TryPython］複数桁のビット演算
3.6　2の補数を求める
3.7　マスクをかえて一部を取り出す
［TryPython］色の成分を取り出す
3.8　ビットをフラグとして利用する
［フラグを操作する］

4⃣コンピュータは論理演算で判断する

4.1　比較演算
［TryPython］比較演算でプログラムの流れを変える
4.2　TrueとFalseを使う論理演算と心理値表
4.3　論理積（AND演算）
［TryPython］論理積（AND演算）を使った成績判定プログラム
4.4　論理和（OR演算）
［TryPython］論理和（OR演算）でYもｙも「はい」と判定する

第３章　方程式で図形を描く

1⃣matplotlibでグラフを描く

［TryPython］グラフを描画する

2⃣方程式からグラフへ

2.1　方程式
［コラム］文字式の書き方
2.2　関数
2.3　関数とグラフ
［TryPython］式を使ってグラフを描画する

3⃣直線の方程式

3.1　2点を結ぶ直線
［TryPython］連立方程式を解く
3.2　直行する2本の直線
［TryPython］点（1、5）を通って直線

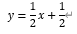
と直交する直線

3.3　2直線の交点
［TryPython］2直線の交点を求める

4⃣比例式と三角比

4.1　比例式の性質
4.2　線分をm:nに内分する点
［コラム］線分の中点を求める方程式
［TryPython］線分を垂直に二等分する直線
4.3　三角比と円
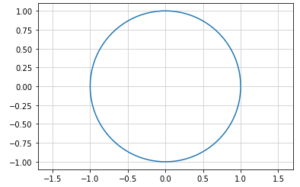
［TryPython］三角比を使って円を描く
［コラム］度数法と弧度法
4.4　三角比と角度
［TryPython］直角を挟む2辺の比から角度を求める

5⃣三平方の定理

5.1　円の方程式
［TryPython］半径rの円を方程式から描画する
［TryPython］円の中心が座標の原点以外の時
5.2　2点間の距離
［コラム］画像から実際の長さを求める方法

6⃣便利な公式

6.1　点から直線までの距離
6.2　直線で囲まれた領域の面積
［コラム］マウスを使って円を描く

第４章　ベクトル

1⃣ベクトルの演算

1.1　ベクトルと矢印
1.2　ベクトルの成分
［コラム］ベクトルの成分を求める
1.3　ベクトルの方向
［TryPython］ベクトルの方向を求める
1.4　ベクトルの大きさ
［コラム］単位ベクトル
1.5　ベクトルの演算
［TryPython］Pythonでベクトルの演算を実行
［コラム］方向も大きさも持たないゼロベクトル
1.6　ベクトルの分解

2⃣ベクトルの方程式

2.1　直線の表し方
［TryPython］2点を結ぶ直線の方程式
2.2　2直線の交点
2.3　ベクトルを使う理由
［コラム］空間図形とベクトル

3⃣ベクトルの内積

3.1　貢献度を計算する
［TryPython］太郎君の貢献度を求める
3.2　仕事の量を計算する
3.3　ベクトルの内積
3.4　2直線のなす角度
［TryPython］2直線のなす角度を求める
3.5　内積の性質
［コラム］コサイン類似度

4⃣ベクトルの外積

4.1　法線ベクトル
［TryPython］ベクトルの外積を求める
4.2　面積を求める
［TryPython］三角形の面積を求める

第５章　行列

1⃣行列とは

1.1　行列の表記方法
1.2　行列の持つ意味
［コラム］本書の行列表記

2⃣行列の演算

2.1　足し算・引き算
［TryPython］行列の足し算と引き算をPythonで実行
2.2　行列の実数倍
［TryPython］行列の実数倍を求める
2.3　掛け算
［TryPython］行列の掛け算を実行してみよう
2.4　掛け算のルール
［TryPython］l×m行列とm×n行列の掛け算
2.5　単位行列
［TryPython］行列×単位行列を計算する
2.6　逆行列
［TryPython］逆行列を求める
2.7　逆行列と連立方程式
［コラム］行列を利用するメリット
［TryPython］逆行列で連立方程式を解く

3⃣図形の一次変換

3.1　ベクトルと行列の関係
［TryPython］ベクトルと行列の掛け算
3.2　図形の対象移動
［TryPython］X軸に対して線対象に変換する
3.3　図形の拡大と縮小
［TryPython］図形を拡大して描画する
3.4　図形の回転
［TryPython］図形を回転させて描画する
［コラム］回転行列ができるまで
3.5　図形の平行移動
3.6　2×2行列から3×3行列へ
［TryPython］図形を平行移動して描画する
3.7　一次変換の組み合わせ
［TryPython］図形を平行移動してから回転させる
［コラム］変換行列を1つにまとめる

第６章集合と確率

1⃣集合

1.1　集合の特徴
［TryPython］Pythonで集合を扱う
1.2　いろいろな集合
1.3　集合とデータベース

2⃣順列と組み合わせ

2.1　場合の数
［コラム］「試行」と「事象」の関係
2.2　場合の数の求め方
［TryPython］集合の要素数
2.3　順列
［TryPython］順列を求めるプログラム
2.4　階乗
［TryPython］階乗の計算はfactorial()関数で
2.5　重複順列
［TryPython］重複順列をプログラムで求める
2.6　組み合わせ
［TryPython］何通りの組み合わせがあるか求める

3⃣確率

3.1　確率の求め方
［TryPython］確率を計算してみよう
3.2　数学的確率と統計的確率
3.3　積の法則と和の法則
3番目にくじを引く人が当たる確率を求める
3.4　モンテカルロ法
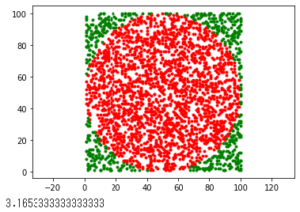
［TryPython］モンテカルロ法で円周率を計算しよう

第７章統計と乱数

1⃣統計とは

1.1　母集団と標本
［TryPyhon］CSVファイルを読み込む
1.2　データのばらつき具合を見る
1.3　平均値、中央値、最頻値
［TryPython］平均値、中央値、最頻値を求めるプログラム
［コラム］NumPyとstatisticsモジュール
1.4　度数分布図
［TryPython］プログラムで度数分布図を作る

2⃣ばらつきを調べる

2.1　分散と標準偏差
［TryPython］分散、標準偏差をプログラムで求める
2.2　偏差値
［TryPython］偏差値をプログラムで求める

3⃣関係を調べる

3.1　散布図
［TryPython］散布図をプログラムで描く
3.2　共分散と相関係数
［TryPython］相関係数を計算する

4⃣データから推測する

4.1　移動平均
［TryPython］移動平均を計算する
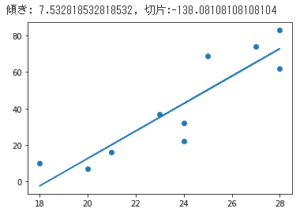
4.2　回帰直線
［TryPython］回帰直線の傾きと切片を求める

5⃣ランダムに値を求める

5.1　乱数
5.2　乱数を使うときに注意すること

第８章微分・積分

1⃣曲線とグラフ

1.1　変化を知る手がかり
［TryPython］年収グラフと差分グラフ
1.2　変化を読み取る

2⃣微分とは

2.1　変化率
2.2　微分係数
2.3　微分する
［コラム］導関数の表記方法
2.4　微分の公式
［TryPython］

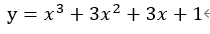
と

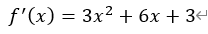
2.5　導関数が教えてくれること
［コラム］極小と極大

3⃣積分とは

3.1　変化を積み重ねる
3.2　積分する
［TryPython］棒グラフの幅と誤差の関係
3.3　定積分・不定積分
3.4　原始関数
［コラム］部分と積分の関係
3.5　積分の公式
［TryPython］

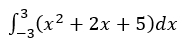
の定積分を求める

3.6積分定数cとは

4⃣道具としての微分・積分

4.1　曲線の接戦
［TryPython］接戦を描画する
［コラム］滑らかな曲線を描画する
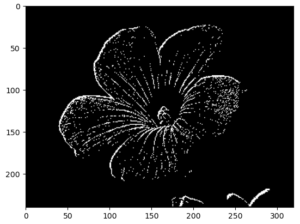
4.2　輪郭の抽出
［TryPython］画像の輪郭をプログラムで抽出する
［コラム］画像の面積を調べる
4.3　円周と円の面積の関係
［TryPython］トイレットペーパーの長さを求める
4.4　円錐の体積
4.5　球の体積と表面積の関係
［TryPython］球の体積と表面積を求める

Appendix ソフトウェア導入ガイド
牽引

※目次を見て頂ければこの本で学べる高校数学の
　単元が一目瞭然です。
　行列は現在高校では教えていませんが、
　コンピュータ、プログラミングを理解する上で
　必須とのことで収録されています。

［TryPython］の実行例

［TryPython］の実行例をいくつか紹介します
【三角比を使って円を描画】

【図形を平行移動してから回転させる】

【モンテカルロ法で円周率を計算しよう】

【回帰直線の傾きと切片を求める】

【画像の輪郭をプログラムで抽出する】

【まとめ】

数学が苦手な人の福音書です。
高校時代全く数学についていけなかった方でも
理解できる内容です。
コンピュータの世界で数学がどのように
応用されているのか理解できます。
Pythonで関数のグラフや図形を描画
しながら数式を通じてプログラミングの初歩的な
勉強にもなります。

著者プロフィール

同志社大学文学部文化学科（現心理学部心理学科）卒。
数学・物理は苦手科目でありながら、在学中に
実験データ解析のためにプログラミングに触れたのを
きっかけにソフトウエア開発の道にすすむことを
決意。ソフトウエア開発会社勤務を経た後、
本格的に書籍の執筆をはじめる。

扱うプログラミング言語はSwift、Java、Python、C、C++、
Delphi、Processing、Scratch、SQLなど多数。
入門者・初心者向けの解説を得意とする。
近年はiOS、Android、MATLABのアプリ開発も
手掛けている。

主な著書は『文系でも必ずわかる中学数学☓Python
超簡単プログラミング入門』（日経BP社）
『改訂3版これからはじめるプログラミング基礎の基礎』
（技術評論社）など。

現在はメディックエンジニアリングで取締役を務める。
メディックエンジニアリングの主な業務は
2次元画像処理、3次元画像計測、機械学習を
キーワードにPC、スマートフォン向けアプリの開発・
販売。ユーザーは官庁や大学の医学部・歯学部・
心理学部、大手化粧品・アパレル会社など幅広い。
一部は海外にも販売している。